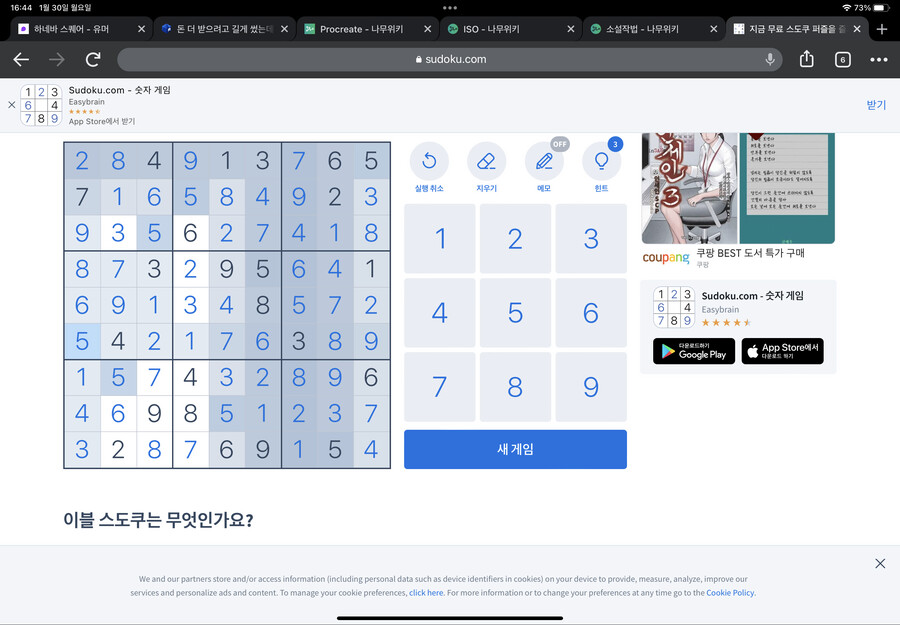
이불 스도쿠입니다
이블이라 쓰여있지만 넘어갑시다
오늘은 이모를 위해 스도쿠를 어떻게 푸는 지 요령을 설명할 거에요
1) 빈칸 채우기 - 쉬움편
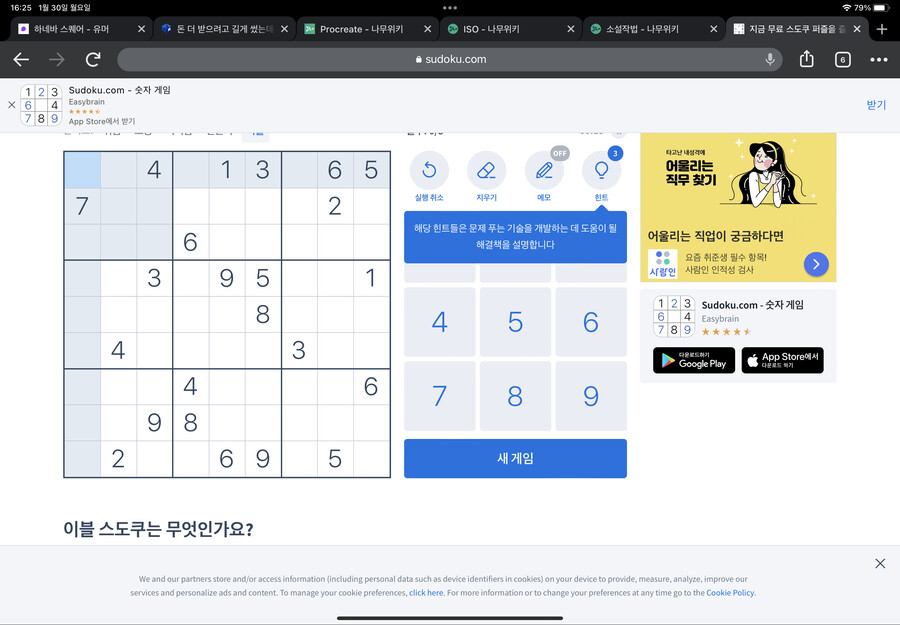
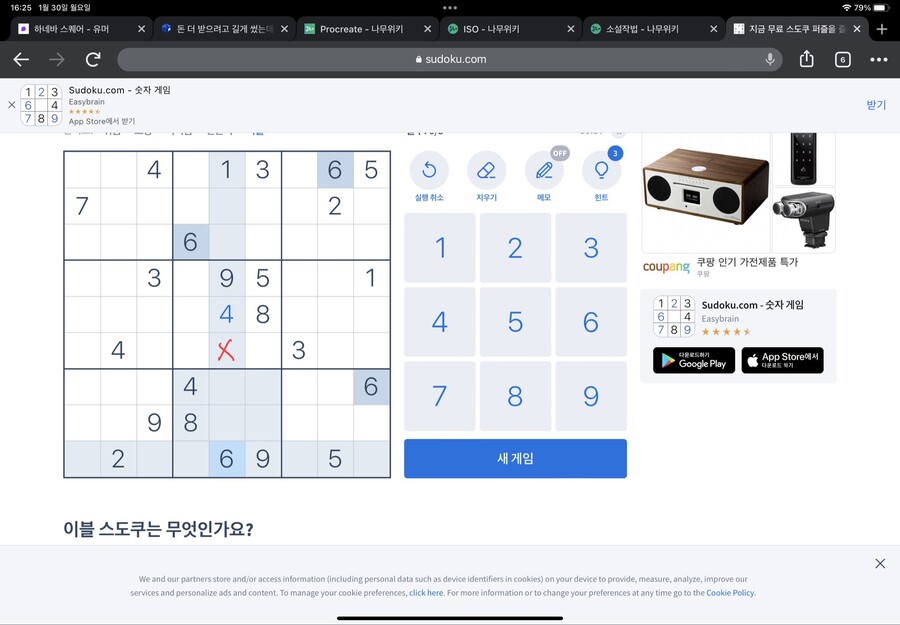
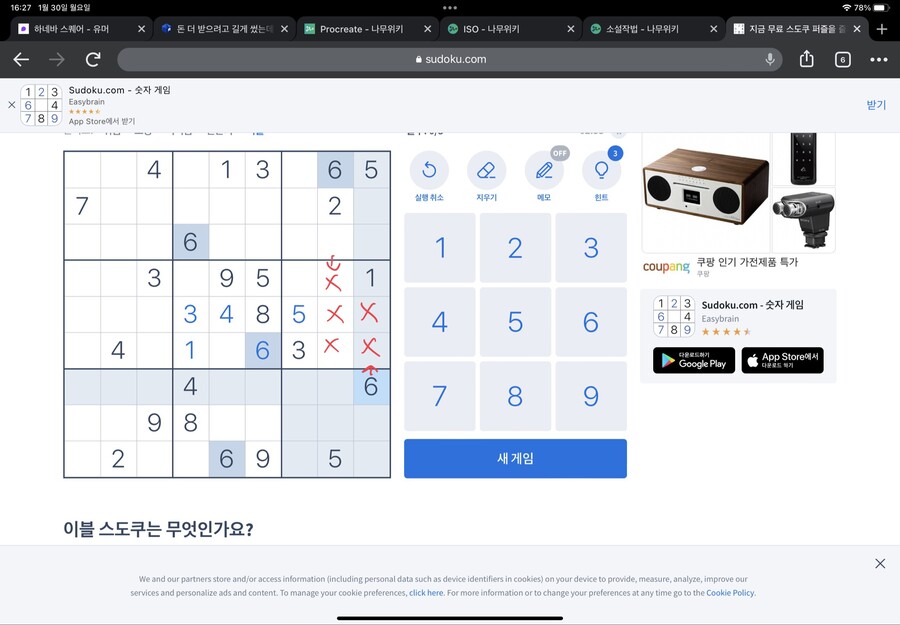
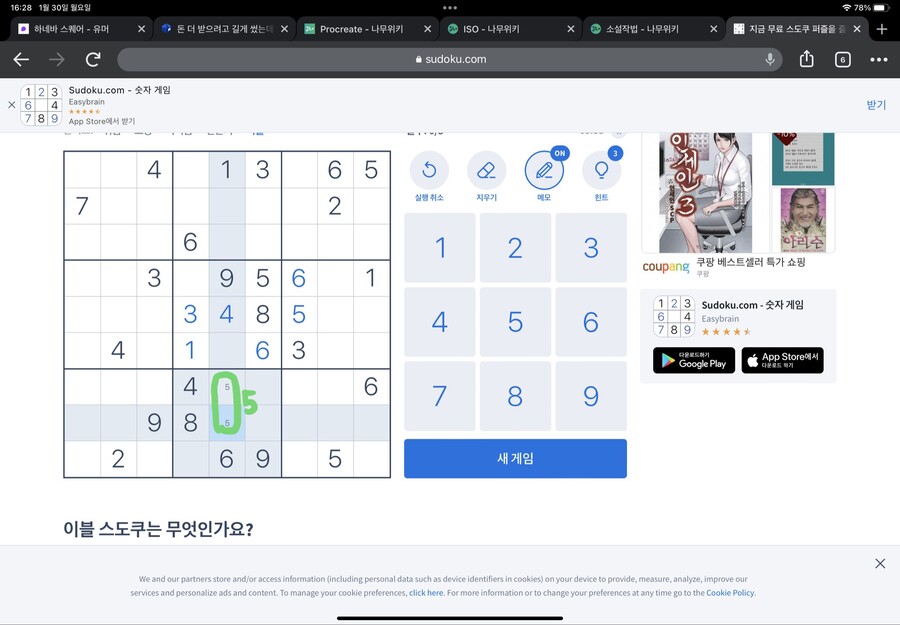
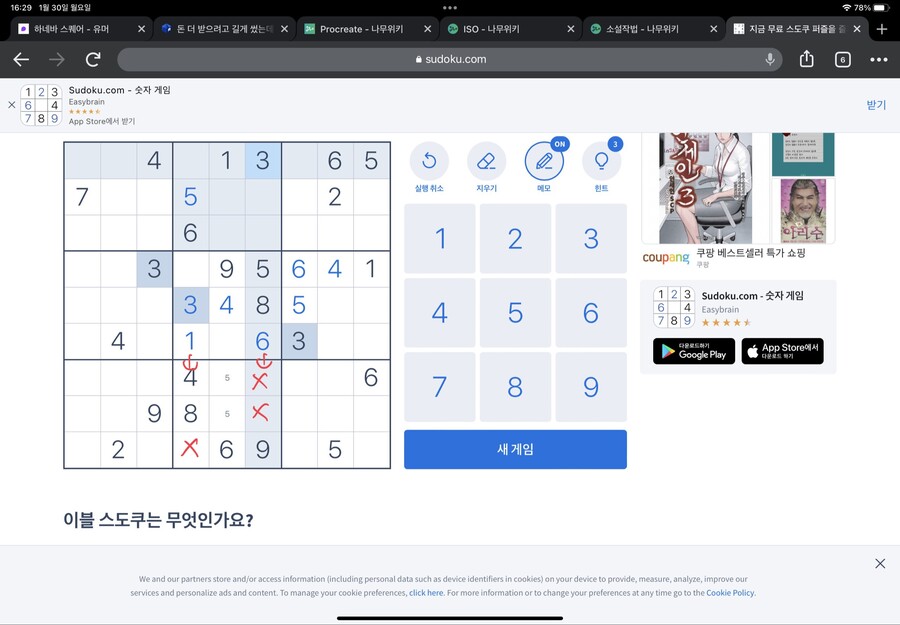
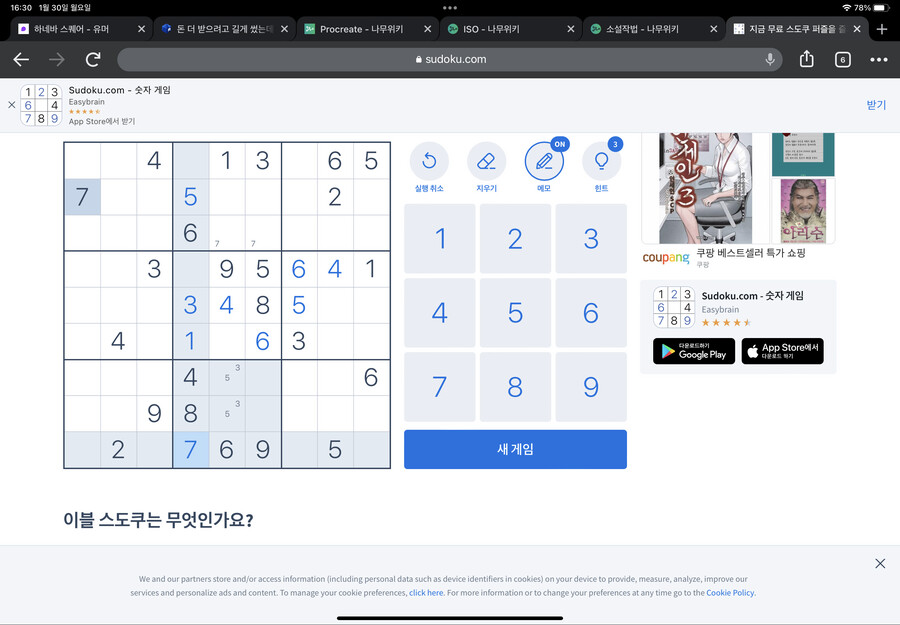
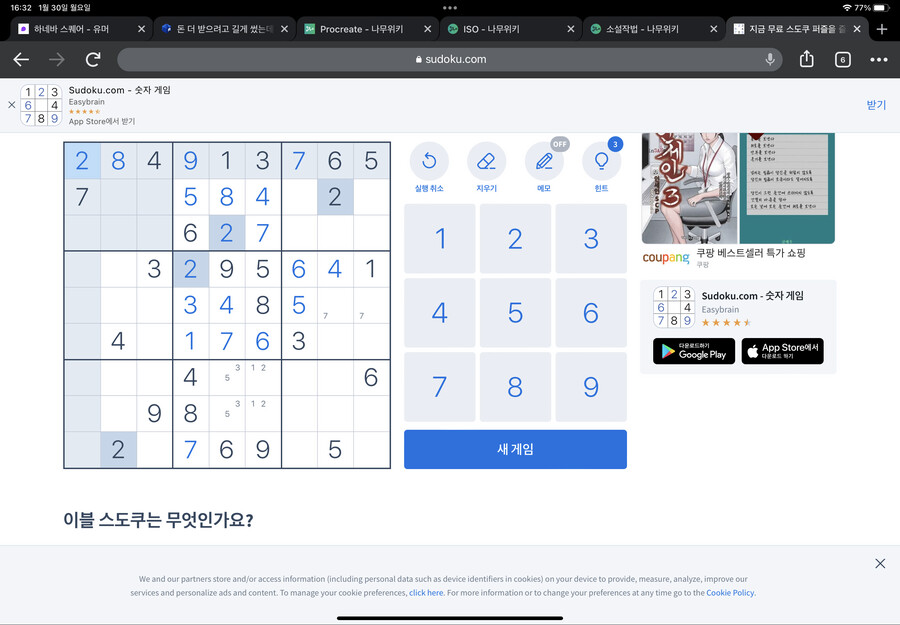
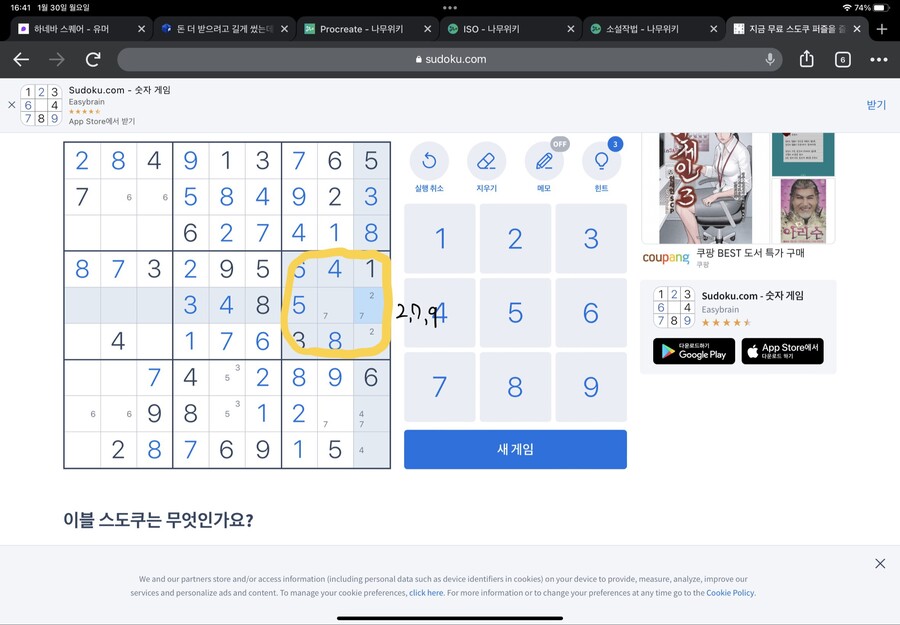
먼저 가운데 네모칸을 봐주세요
하단 네모칸의 4가 저 위치에 있어서
가운데 네모칸에는 4가 들어가면 안되는 위치가 저렇게 됩니다(빨간 X표시 친 부분)
마찬가지로 좌측편의 네모칸의 4가 저 위치에 있어서
>가운데 네모칸에는 4가 들어가면 안되는 위치가 저렇게 됩니다(빨간 X표시 친 부분)
그럼 가운데 네모칸의 4는 어디 들어가야 할까요?
바로 정가운데입니다
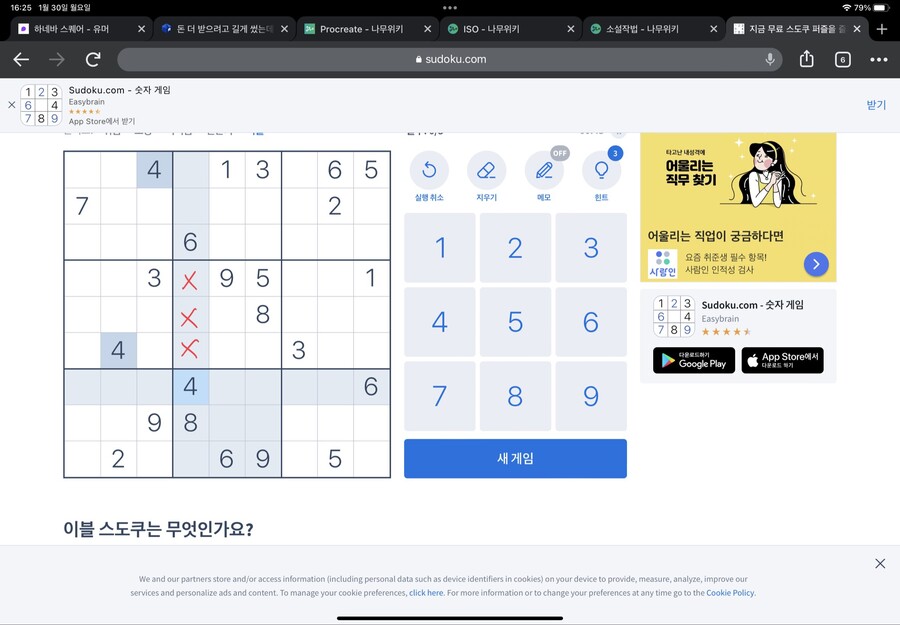
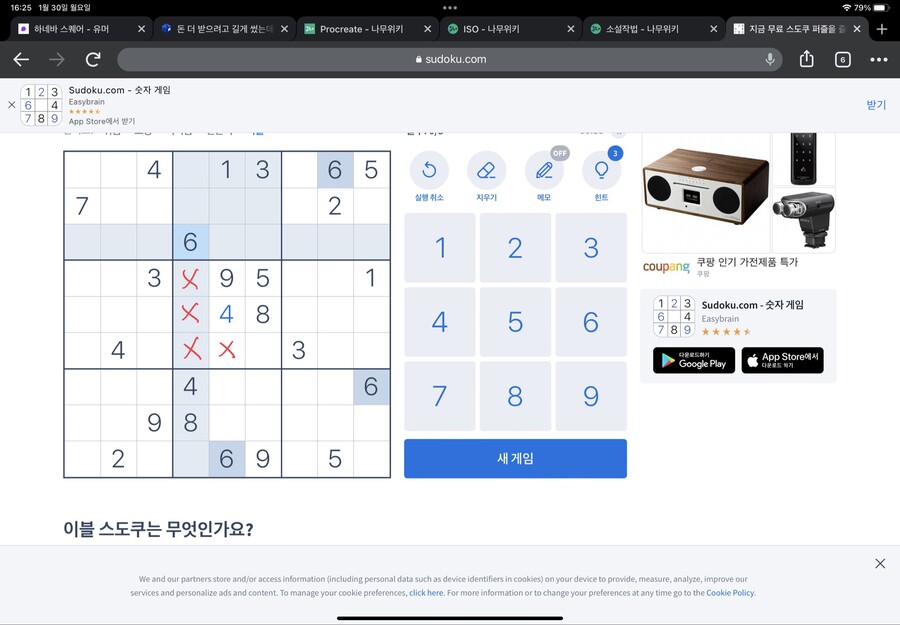
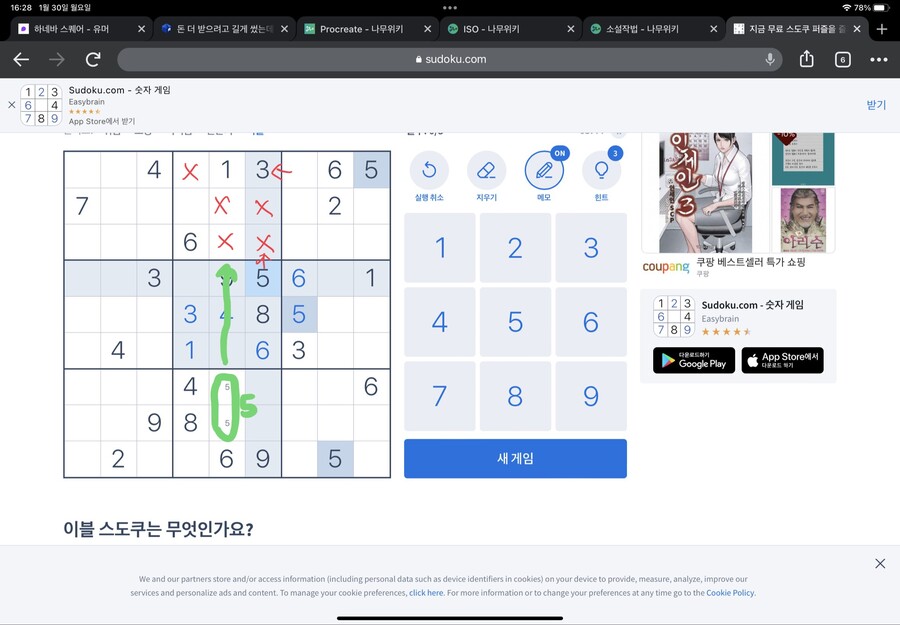
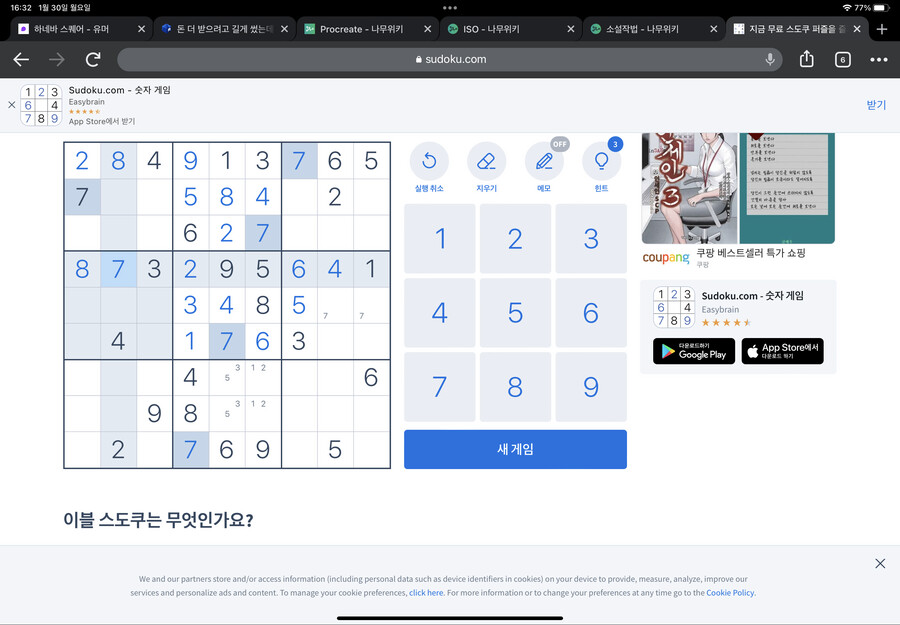
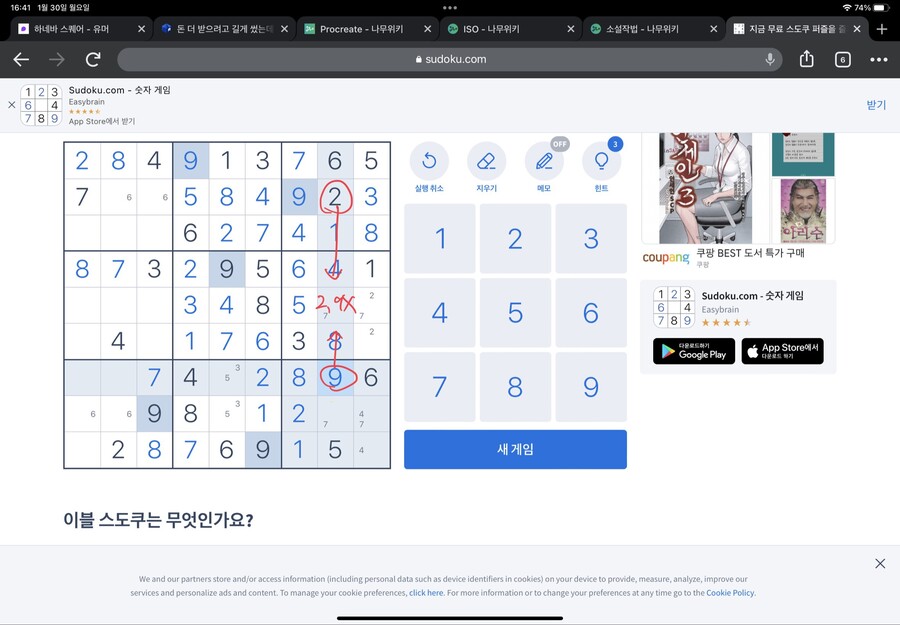
이걸 같은 네모칸의 6에 적용해봅시다
이렇게 가운데 네모칸에 들어갈 수 없는 6의 자리를 칠하면 한 자리가 남습니다
그 자리에 6이 들어갑니다
참 쉽죠?
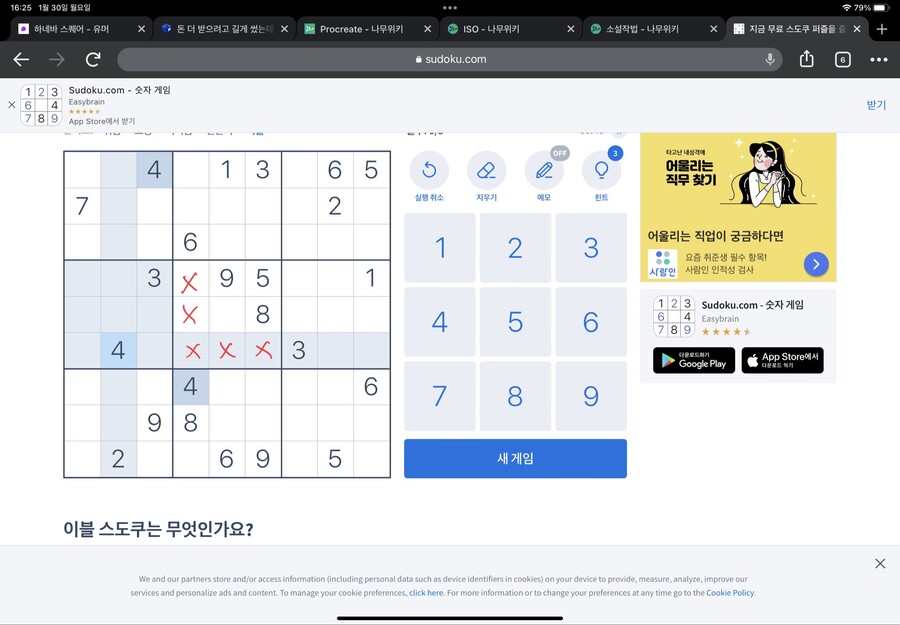
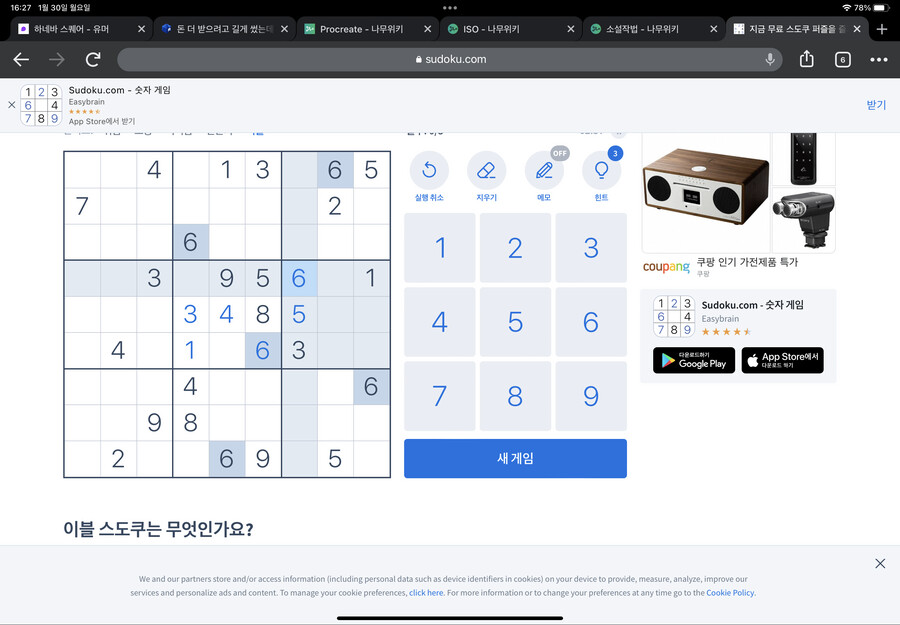
이번엔 오른쪽 네모를 봅시다
5가 들어갈 수 없는 위치를 체크 한 뒤 남은 자리를 보니 한 자리입니다
5는 그 자리에 들어갑니다
마찬가지로 오른쪽 네모칸에 6이 들어가면 안되는 자리를 표시해보면?
6도 한자리가 남습니다
바로 그 자리가 6이 들어갈 자리입니다
이렇게 말이죠
2) 어 근데 숫자가 이제 안들어가는 거 같은데 이래도 숫자를 찾을 수 있나요?
대답부터 먼저 하자면 예
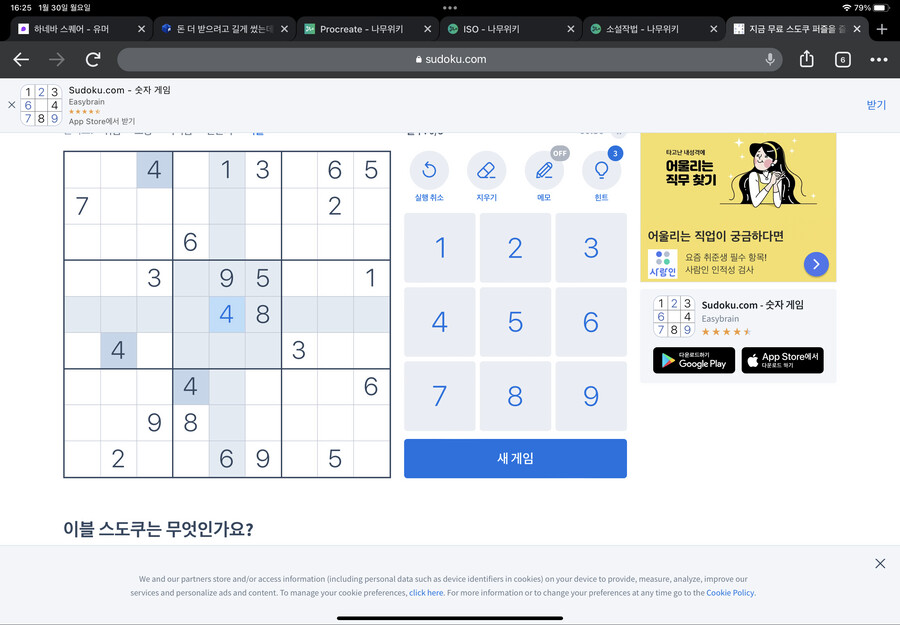
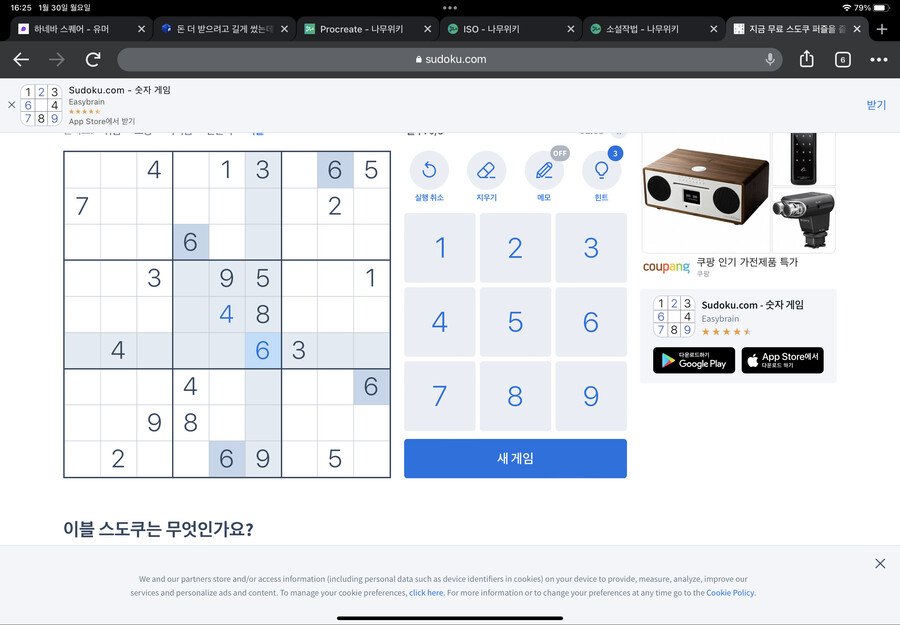
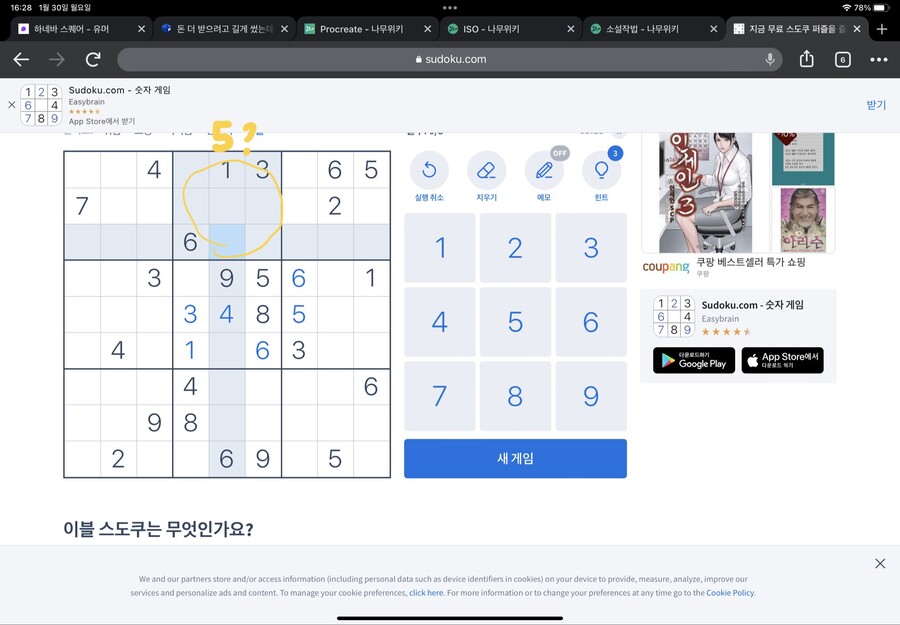
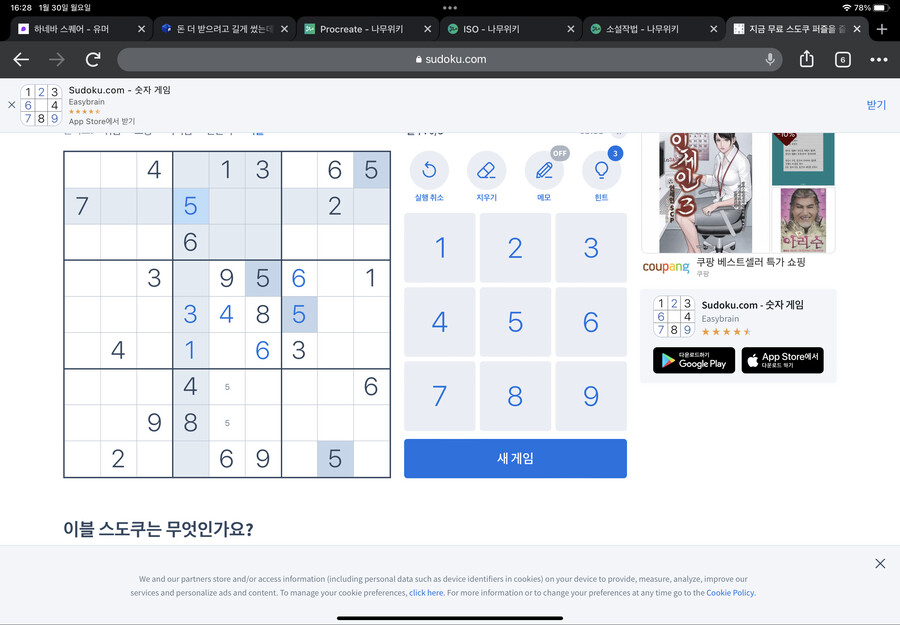
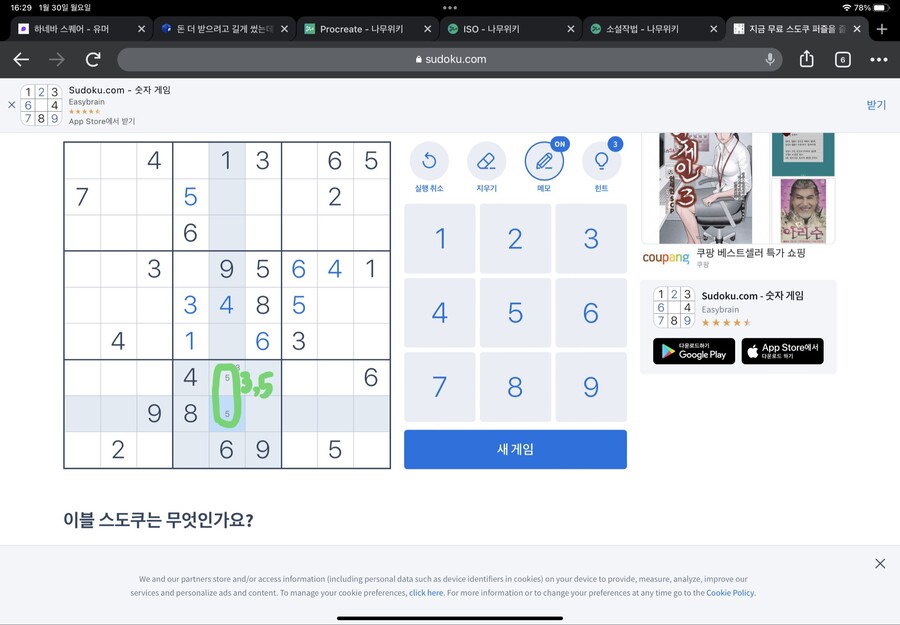
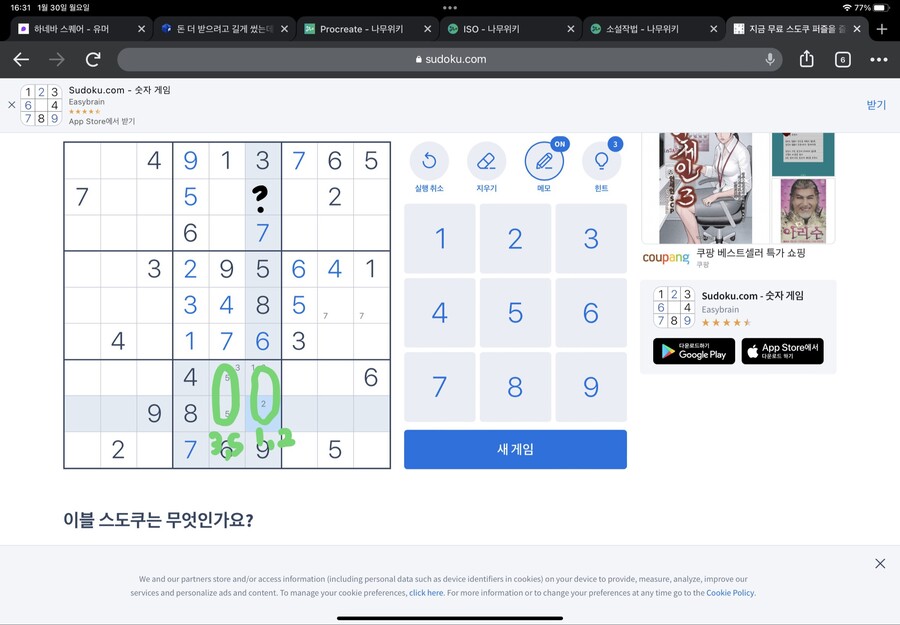
위 네모칸을 먼저 봅시다
위 네모칸에 5를 어디 넣어야 할까요?
1의 방법만 사용하기엔 정보가 부족합니다
하지만 아래쪽 네모칸에 주목하면,
5는 X표 쳐지지 않은 두 칸중 하나에 들어간다는 걸 알 수 있습니다
5가 어디에 들어가던,
위 네모칸의 가운데 세로열에는 5가 들어갈 수 없다는 걸 알 수 있습니다
처음 찾은 정보랑 합쳐서 X표를 치면…
5가 들어갈 곳이 정해진다는 걸 알 수 있습니다
저기에 5가 들어가야겠죠
3) 숫자 묶기
3은 2를 심화한 내용입니다
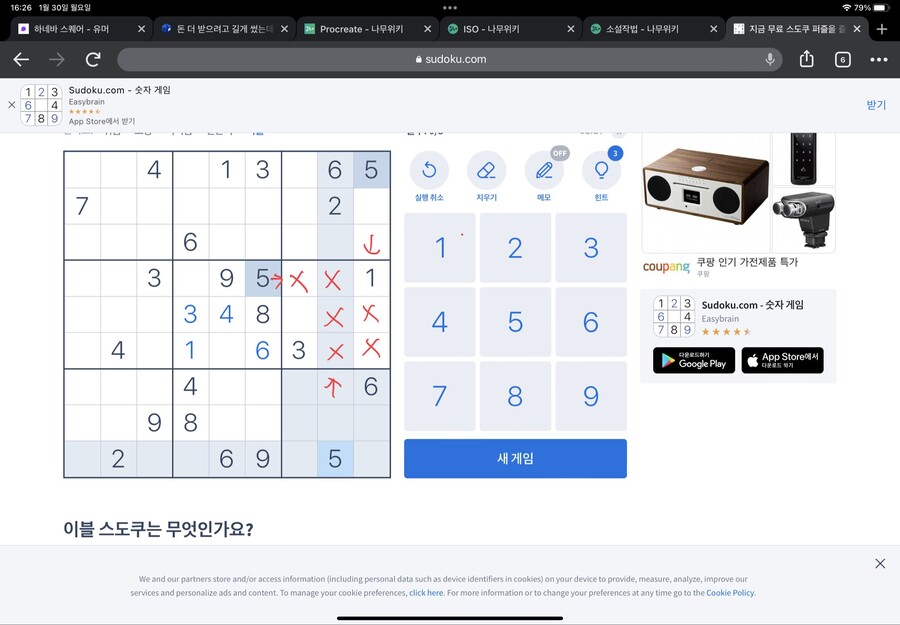
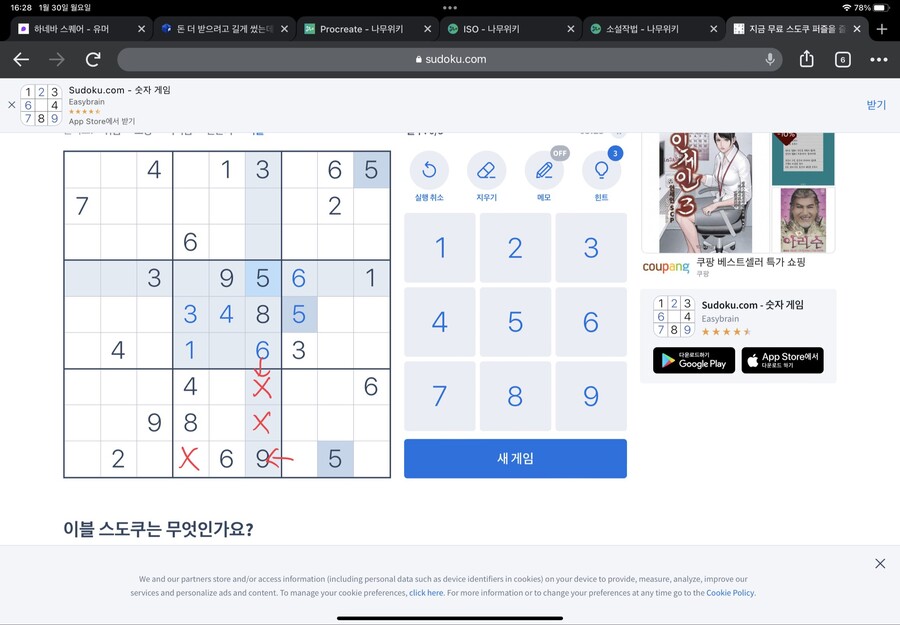
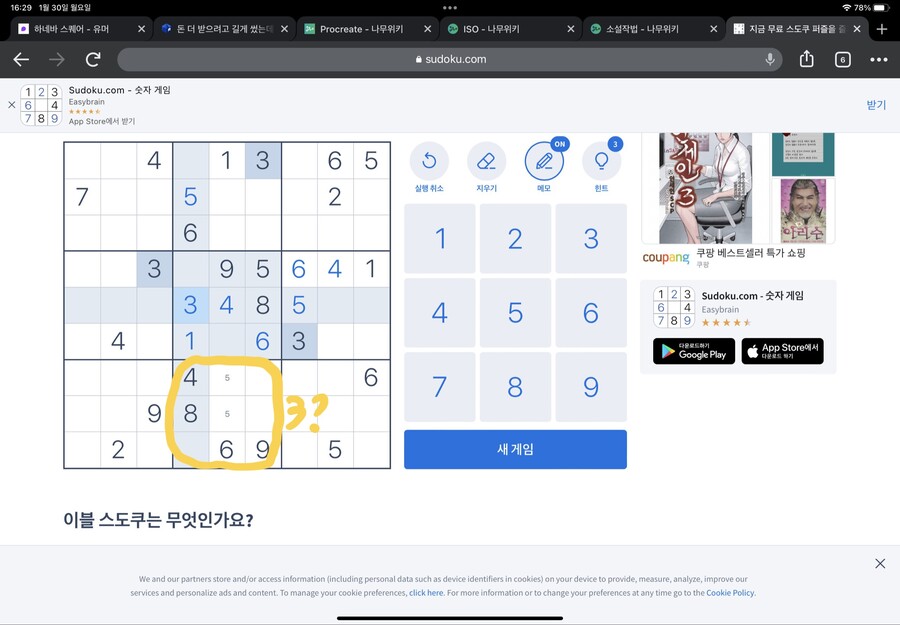
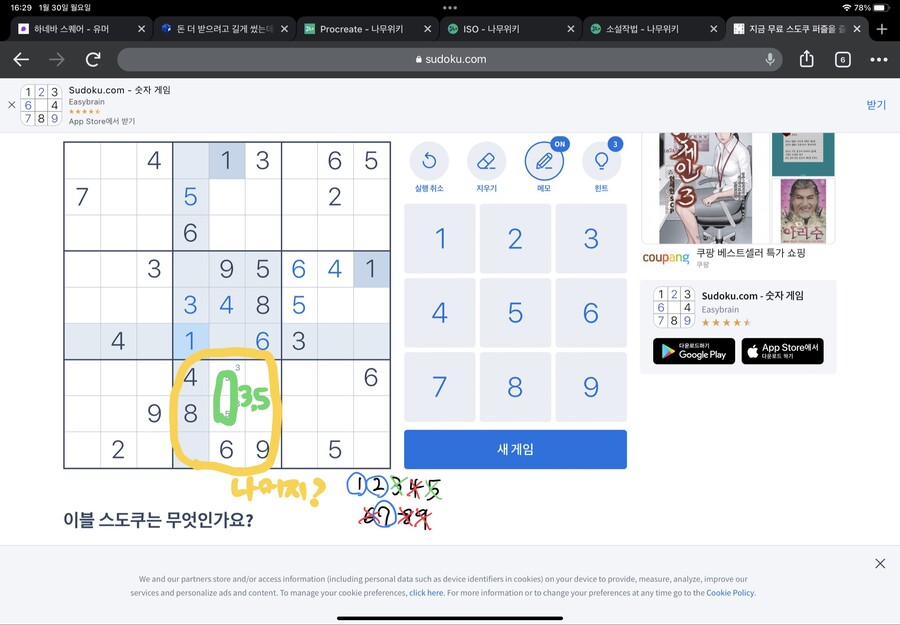
다시 아래 네모칸에 주목하봅시다
아래 네모칸에서 3은 어디 들어가야 할까요?
X표 치고 보면 두칸이 남습니다
그런데 잘보면
아까 5가 들어갈 수 있는 곳이랑 같습니다
그렇습니다 3 아니면 5밖에 못 들어간 다는 걸 알 수 있습니다
그럼 아래 네모칸에서 3,5 제외하고 남은 숫자는 뭐가 있을까요?
1,2,7이 남아있네요
그런데 주변을 보니
바로 위에 1이, 왼편에 2가 있습니다
그럼 저기 저 칸에는..
7이 들어가야 하는 겁니다
아까 3,5가 한 묶음으로 취급되니,
나머지 두칸은 자연히 1,2가 한묶음이 되는 겁니다
그럼 1,2가 한 묶음이 되니 위칸의 검은 물음표 칸에 시선이 모이겠죠?
아마 여기까지 잘 온 이모라면 나머지 숫자 하나를 유추할 수 있을 거라 생각해요
그리고, 마찬가지로 밑에 3,5가 한 묶음이니 위에 네모칸의 나머지 두칸도 풀 수 있을 거고요
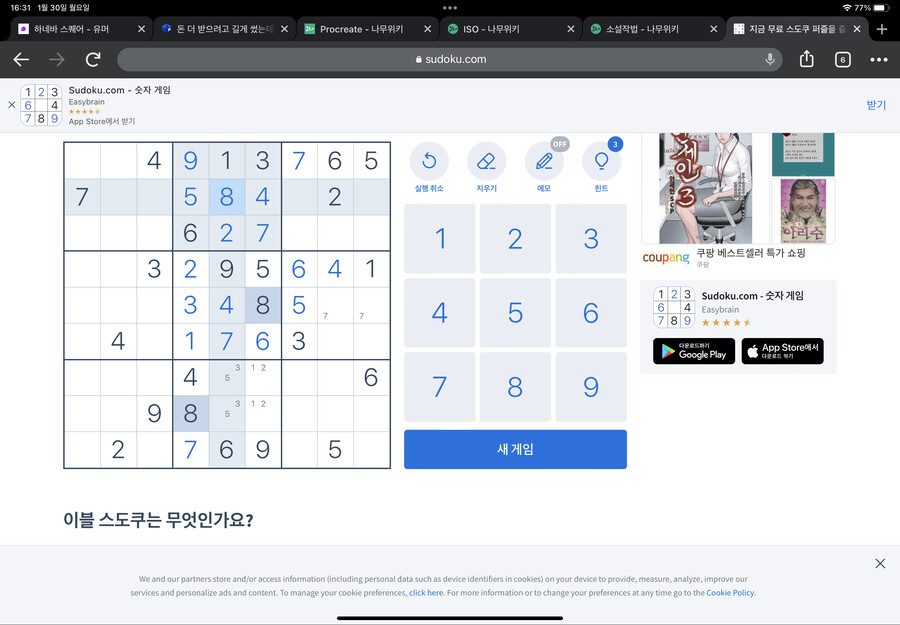
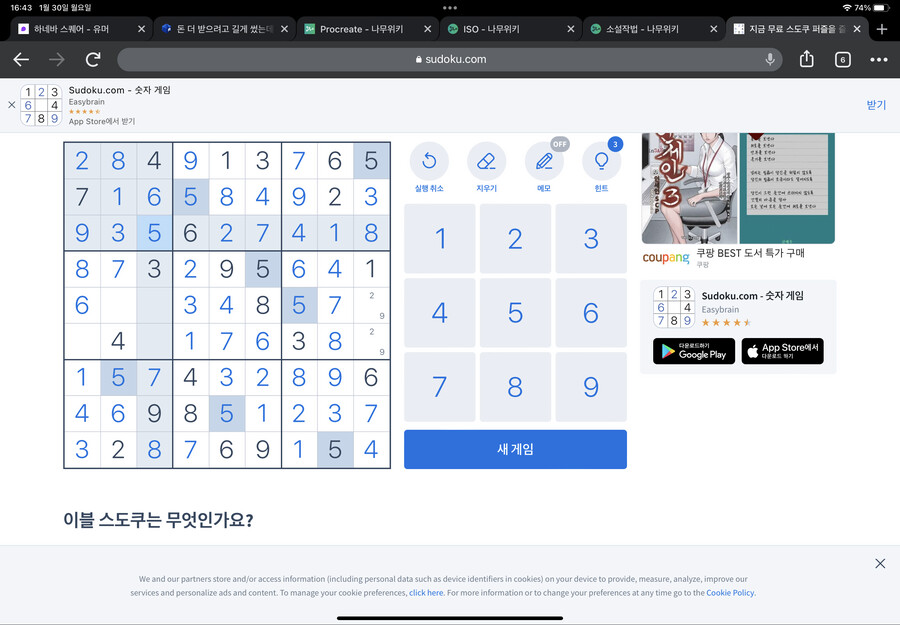
정상적으로 풀었다면 아마 이런 결과가 나올 거에요
그러면 맨 위 가로줄은 풀수가 있을 거고요
잘 따라오고 있다면 여기도 잘 하실 거에요
1에서 했던 걸 떠올리면서 왼쪽 아래 네모칸에 7이랑 8이 어디에 들어갈지 찾을 수 있겠죠?
4) 복합
여기는 1),2),3) 셋다 섞어서 풀어야 이해가 되는 곳이니
하나라도 제대로 숙지가 안되면 쓸 수 없는 방법이에요
숙지가 안됬으면 다시 위로 올라가시면 되요
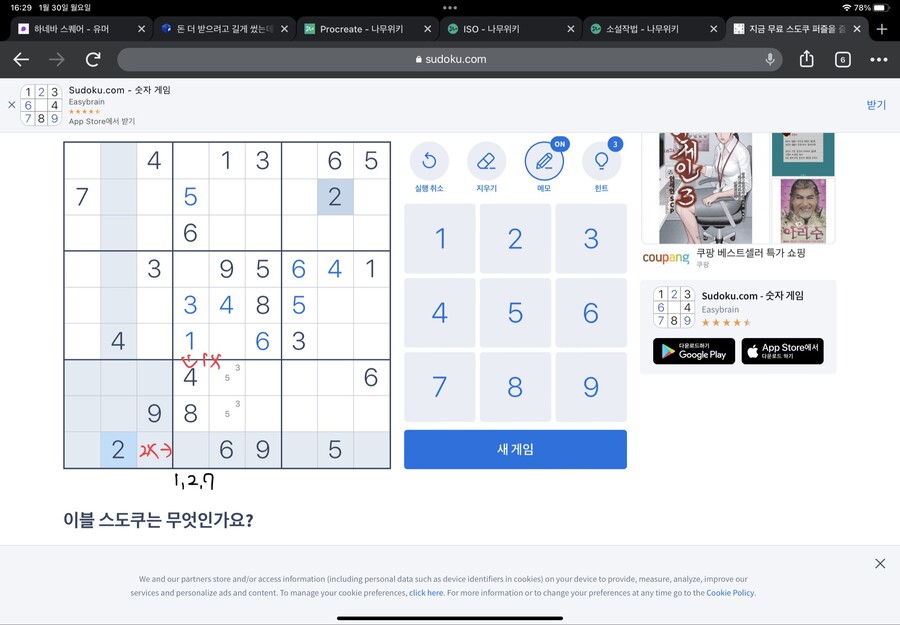
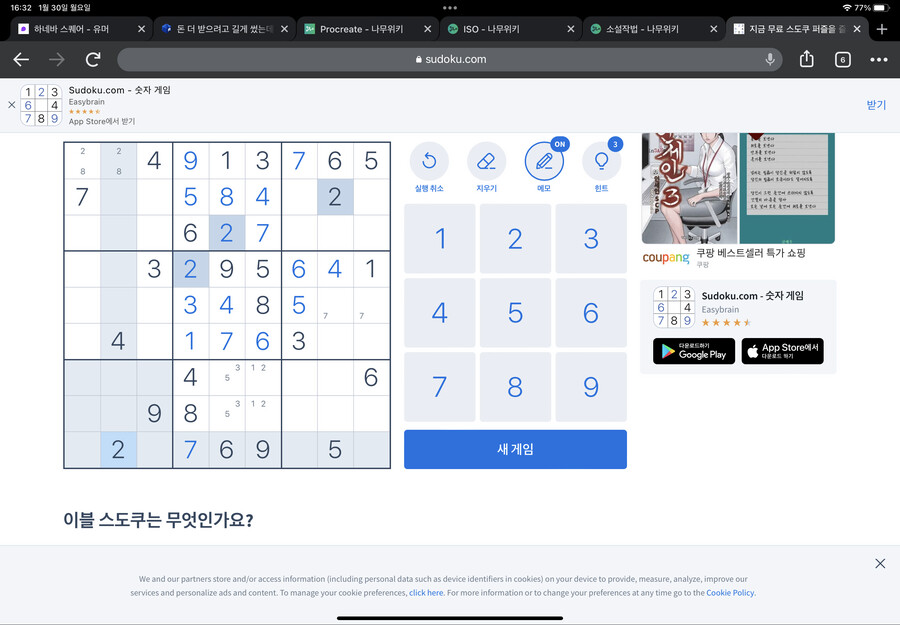
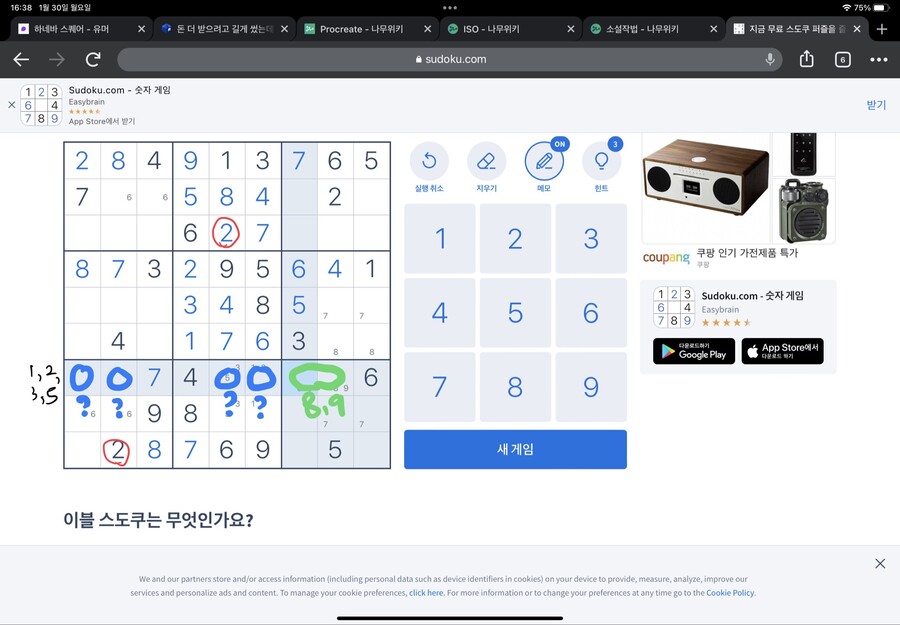
밑에서 3번째 가로 줄에 주목하면
오른쪽 아래 네모칸에 8,9가 묶어서 들어가야 하고
나머지 넷의 숫자를 정해야 합니다
잘 세어보니 1,2,3,5가 들어가야 합니다
여기서 숫자 2에 주목해봅시다
숫자 2가 왼쪽 아래 네모칸에 들어가 있고,
또 위 네모칸 가운데 세로줄에 들어가 있습니다
그럼 2가 들어갈 수 있는 곳은?
딱 한 곳이 됩니다
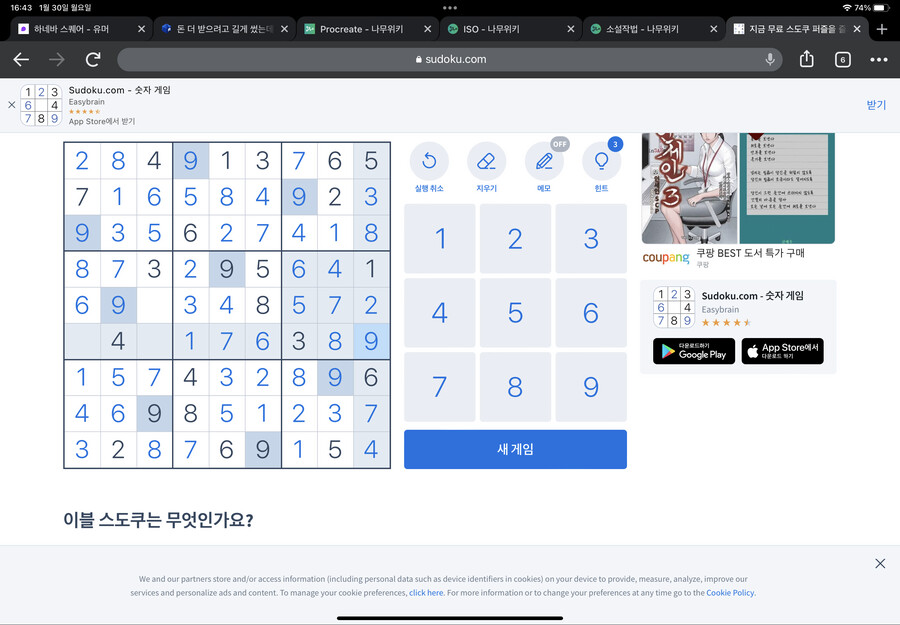
잘 따라오고 있다면 이런 그림이 나올 겁니다
그럼 이제 이모가 1),2),3)에서 썼던 걸 토대로 노란색 동그라미 친 곳의 숫자를 채워보면 됩니다
5) 소거
소거는 말 그대로 지운다는 의미의 단어입니다
여기서는 어떻게 쓰이는 지 알아봅시다
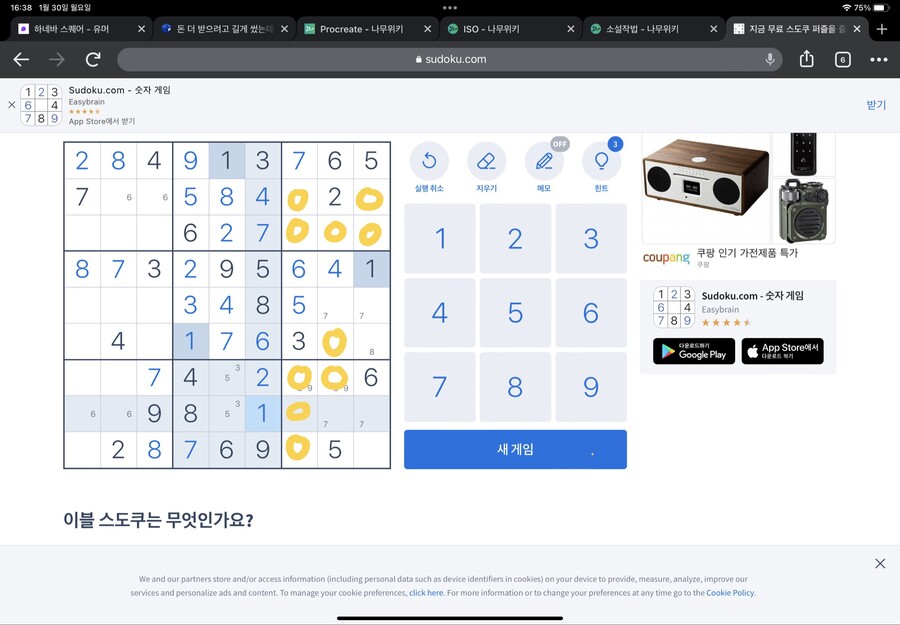
노란색 동그라미 친 오른쪽 네모칸에 주목해봅시다
들어가야 할 숫자는 2,7,9가 들어가야 합니다
오른쪽에서 2번째 세로줄을 유심히 보니 2랑 9가 있습니다
근데 우리는 2,7,9중 하나를 빈곳에 넣어야 하고요
그럼 저 칸에 뭐가 들어가야 할까요?
그렇죠 7이 들어가야 하죠
*사실 3)보다 쉬운데
왜 지금 나오는 지는 묻지맙시다…;;;
6) 여기까지 왔다면?
정말 다 왔습니다
차근히 숫자를 채워주시면 됩니다
어때요, 참 쉽죠?
7) 이런 기술은 어려운 난이도에서도 써먹을 수 있나요?
네
일단 소거법도 4칸 이상의 빈칸에서 쓸 수 있고
수 묶음도 셋이상 묶는 게 가능합니다
하지만 보통 이 경지에 오면 문제가 미친듯이 어렵다던가
위의 방법들이 다 안 통해서 얻은 정보를 활용해서 가설을 세운 뒤 저 가설이 틀렷는지 입증하는 방법으로 풀어야 하는 정도라
이모 머리가 녹아내릴 가능성이 높읍니다
당장 X자 모양 스도쿠도 그렇게 푼거…
아무튼 필력이 부족한 편인데
이모에게 도움이 될 수 있었으면 하는 바람에서
학부생이 글 올립니다